Wyszukaj
Zaloguj / zarejestruj się
Jeśli masz już konto, możesz się zalogować.
Jeśli nie masz konta, zarejestruj nowe podając nazwę użytkownika, adres email i hasło.
Formularz kontaktowy
Memorizer+
Wykup dostęp
Ta funkcja jest dostępna dla użytkowników, którzy wykupili plan Memorizer+
Fiszki
Prognozowanie procesów ekonomicznych
Test w formie fiszek Pytania z podręcznika "Prognozowanie ekonomiczne, teoria przykłady zadania"
Ilość pytań: 108 Rozwiązywany: 16033 razy
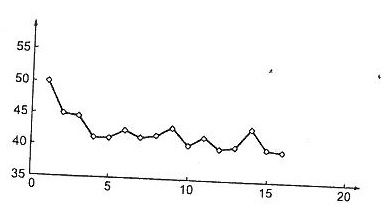
Na rysunku przedstawiono wykres szeregu czasowego pewnej zmiennej. Na jego podstawie możemy stwierdzić, że w szeregu tym występuje:
tylko składowa przypadkowa
trend hiperboliczny i wahania przypadkowe
trend liniowy i wahania przypadkowe
O istnieniu trendu wykładniczego można mówić wówczas, gdy na wykresie wzdłuż linii prostej układają się punkty o współrzędnych:
( t, ln yt )
( lnt, yt )
( e^2, yt )
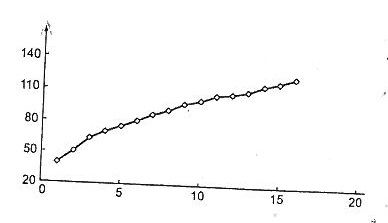
Na rysunku przedstawiono wykres szeregu czasowego pewnej zmiennej. Na jego podstawie możemy stwierdzić, ze w szeregu tym występuje:
składowa systematyczna w postaci trendu potęgowego oraz składowa przypadkowa
składowa systematyczna w postaci trendu liniowego oraz składowa przypadkowa
tylko składowa systematyczna
O istnieniu trendu potęgowego można mówić wówczas, gdy na wykresie wzdłuż linii prostej układają się punkty o współrzędnych:
( ln t, yt )
( t, ln yt )
( ln t, ln yt )
Za paraboliczną postacią trendu przemawiają w miarę stałe:
drugie przyrosty absolutne o podstawie stałej badanego zjawiska
drugie przyrosty względne o podstawie zmiennej badanego zjawiska
drugie przyrosty absolutne o podstawie zmiennej badanego zjawiska
Za wykładniczą postacią trendu przemawiają w miarę stałe:
indeksy o podstawie stałej, przy czym podstawą jest okres, dla którego zjawisko przyjmuje najmniejszą wartość
indeksy łańcuchowe
przyrosty względne o podstawie zmiennej badanego zjawiska
Za liniową postacią trendu przemawiają w miarę stałe:
przyrosty absolutne o podstawie stałej badanego zjawiska
przyrosty absolutne o podstawie zmiennej badanego zjawiska
przyrosty względne o podstawie zmiennej badanego zjawiska
W celu oszacowania parametrów funkcji trendu f(t) = t / a0 + a1t odpowiedni model sprowadzamy do postaci liniowej przez następującą transformację zmiennej y oraz t:
lny oraz 1/t
1/y oraz 1/t
modelu z taką funkcją trendu nie da się sprowadzić do postaci liniowej
Szereg czasowy przedstawia wartości pewnej zjawiska co kwartał. Na podstawie analizy graficznej jego przebiegu stwierdzamy, że co cztery kwartały wykazuje on podobne własności, zatem:
charakteryzuje się cyklem rocznym
charakteryzuje się wahaniami o okresie 4 kwartaly, czyli o okresie rocznym
charakteryzuje się wahaniami o okresie 1 kwartał
Metoda trendów jednoimiennych okresów polega na:
oszacowaniu parametrów funkcji trendu oddzielnie dla poszczególnych faz cyklu
oszacowaniu wskaźników sezonowości dla poszczególnych faz cyklu
oszacowanie parametrów funkcji trendu oddzielnie dla każdego cyklu
Do opisu szeregu czasowego zawierającego obserwacje z 24 kwartałów pewnej zmiennej wybrano analizę harmoniczną, czy:
pierwsza harmonika ma okres 6 lat
szósta harmonika ma okres 1 roku
należy oszacować parametr 12 harmonik
Suma bezwględnych wahań sezonowych (oczyszczonych)
zawsze jest równa 100%
zawsze jest równa zeru
zależy od tego, czy rozważamy wahania półroczne, kwartalne czy miesięczne
Suma wskaźników sezonowości (oczyszczonych)
zawsze jest równa 1
zawsze zależy od liczby cykli
jest równa 4 w przypadku wahań kwartalnych
Suma wskaźników sezonowości (oczyszczonych) w przypadku wahań miesięcznych
jest równa 12%
jest równa 12
jest równa 1200%
Suma oczyszczonych bezwzględnych wahań sezonowych (model addytywny) w przypadku wahań miesięczny
zależy od liczby cykli
jest równa 12
jest równa 0
Patrz obrazek
z kwartału na kwartał produkcja cementu średnio wzrstałą o 25,9 [tys. ton]
z roku na rok produkcja cementu średnio wzrastała o 25,9 [tys. ton]
z kwartału na kwartał produkcja cementu przeciętnie wzrastała o 25,9 %

prognozy nie można wyznaczyć, ponieważ nie jest znany bezwzględny wskaźnik sezonowości dla czwartego kwartału
prognoza produkcji cementu na czwarty kwartał 1997 r. wynosi 3365,52 [tys.ton]
prognoza produkcji cementu na czwarty kwartał 1997 r. wynosi 2951,52 [tys.ton]

Wykorzystując liniowy lub sprowadzalny do postaci liniowej model przyczynowo-opisowy można:
Ocenić siłę wpływu poszczególnych zmiennych na zmienną prognozowaną
Oszacować ex ante błędy wyznaczonych na jego podstawie prognoz
Na jego podstawie uzyskać prognozy wariantowe
Wady modelu przyczonowo-opisowego to:
Możliwość obliczenia prognoz wariantowych
Problemy przy estymacji parametrów związane z możliwością wystąpienia zjawiska współliniowości
Potrzeba wyznaczenia wartości zmiennych objaśniających w okresie na który buduje się prognozy
W celu wyboru postaci związku funkcyjnego f między zmienną objaśnianą a zmiennymi objaśniającymi przy budowaniu prognostycznego modelu przyczynowo-opisowego możemy wykorzystać:
Istniejącą teorię na temat prognozowanego zjawiska
Współliniowość zmiennych objaśniających
Analizę materiału statystycznego

Cześć!
Wykryliśmy, że blokujesz reklamy na naszej stronie.
Reklamy, jak zapewne wiesz, pozwalają na utrzymanie i rozwój serwisu. W związku z tym prosimy Cię o ich odblokowanie by móc kontynuować naukę.
