Wyszukaj
Zaloguj / zarejestruj się
Jeśli masz już konto, możesz się zalogować.
Jeśli nie masz konta, zarejestruj nowe podając nazwę użytkownika, adres email i hasło.
Formularz kontaktowy
Memorizer+
Wykup dostęp
Ta funkcja jest dostępna dla użytkowników, którzy wykupili plan Memorizer+
Fiszki
Informatyka Stosowana
Test w formie fiszek egzamin, systemy operacyjne, Bazy danych, obrazy, programowanie, sieci
Ilość pytań: 156 Rozwiązywany: 5370 razy
Przekształceniem geometrycznym nie jest:
b) przesunięcie obrazu,
d) zmiana wielkości obrazu.
c) binaryzacja obrazu,
a) obrót obrazu,
Rozpatrujemy następujący obraz szary: 55 56 57 Jaki zmieni się ten obraz po operacji rozszerzenia zakresu histogramu (zakres poziomów szarości od 0 do 255)?
55 56 57
0 57 255
0 255 56
0 255 127
Rozpatrujemy obraz szary 15 45 22 20 48 35 13 12 56 Jaki będzie wynik binaryzacji tego obrazu z dolnym progiem wynoszącym 30?
0 15 0/0 18 5/0 0 26
45 75 55/50 78 65/43 42 26
101/110/ 110
010/011/001
Macierz konwolucji: 111 121 111 Jest wykorzystywana do:
d) Filtracji dolnoprzepustowej mającej na celu znaczne rozmycie konturów obiektów.
b) Filtracji górnoprzepustowej mającej na celu wykrycie punktów izolowanych,
a) Filtracji górnoprzepustowej mającej na celu wykrycie krawędzi,
c) Filtracji dolnoprzepustowej mającej na celu minimalizacje rozmycia konturów obiektów,
Laplasjan służy do:
d) wykrywania narożników obiektów.
a) usuwania szumów w obrazie,
c) wykrywania wszystkich konturów obiektów,
b) wykrywania poziomych i pionowych konturów obiektów,
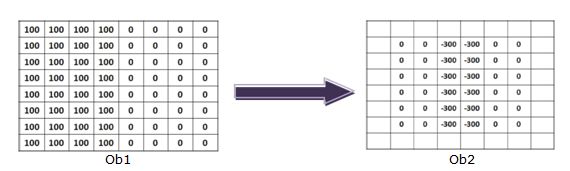
W wyniku filtracji obrazu Ob1 otrzymano obraz Ob2 (obraz przed normalizacją): Jakiego filtru użyto w tej operacji?:
c) Robertsa,
b) gradientu morfologicznego,
a) uśredniającego,
d) Prewitta.
Rozpatrujemy przekształcenia morfologiczne: erozja, dylatacja, otwarcie, zamknięcie (przy wykorzystaniu tego samego elementu strukturalnego, na tym samym obrazie wejściowym). Jakie związki zachodzą między wynikami tych operacji?
b) dylatacja ≥ zamknięcie ≥ obraz wejściowy ≥ otwarcie ≥ erozja
d) dylatacja ≥ erozja ≥ obraz wejściowy ≥ zamknięcie ≥ otwarcie
c) zamknięcie ≥ otwarcie ≥ obraz wejściowy ≥ dylatacja ≥ erozja
a) obraz wejściowy ≥ erozja ≥ dylatacja ≥ otwarcie ≥ zamknięcie
Rozpatrujemy obraz: oraz element strukturalny W wyniku operacji Hit-or-Miss, dla piksela zaznaczonego czarną obwódką, otrzymamy wartość:
1
5
4
0

Które stwierdzenie nie jest prawdziwe?
a) Erozję obrazu można otrzymać wykonując dylatację dopełnienia obrazu a następnie wykonując dopełnienie obrazu będącego wynikiem tej operacji.
d) Erozję wykorzystuje się do otrzymania funkcji dystansu
c) Jeżeli punkt centralny należy do elementu strukturalnego, to wynik erozji obrazu binarnego zawiera się w obrazie przed erozją,
b) Jeżeli na obrazie wykonamy erozję, a następnie na otrzymanym wyniku wykonamy kolejną erozję takim samym elementem strukturalnym, to w rezultacie drugiej operacji na otrzymamy żadnych zmian.
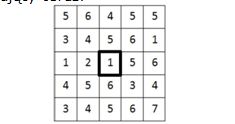
Rozpatrujemy następujący obraz: Jaką wartość będzie miał piksel otoczony ciemną obwódką po operacji otwarcia obrazu elementem strukturalnym w kształcie kwadratu o rozmiarze 3x3, z punktem centralnym w jego środku.
5
3
1
7
Zamknięcie służy m.in. do:
c) rozłączenia obiektów leżących blisko siebie,
b) usunięcia małych obiektów,
a) usunięcia otworów w obiektach,
d) wykrycia konturów obiektów.
Jeżeli od obrazu odejmiemy obraz będący wynikiem filtracji tego obrazu otwarciem morfologicznym wykorzystującym stosunkowo duży element strukturalny, to:
c) otrzymamy obraz ze wzmocnionymi krawędziami,
d) usuniemy z obrazu efekt nierównomiernego oświetlenia.
b) otrzymamy obraz gradientu morfologicznego,
a) otrzymamy obraz uśredniony, pozbawiony szumów,
Po transformacji Fouriera otrzymano piksel o wartości 3+4i. Jaka jest wartość modułu tego piksela?
6
3
4
5
W wyniku transformacji Fouriera obrazu Ob1 otrzymano obraz, na którym wycięto składowe odpowiadające za niskie częstotliwości(jak na obrazie Ob2). Jak będzie wyglądał rezultat odwrotnej transformacji Fouriera obrazu Ob2 ?
d
a
b
c

) Na obrazie szarym (poziomy szarości z przedziału 0-255) przeprowadzono transformację Fouriera, wymnożono f-obraz przez charakterystykę filtru oraz wykonano na wyniku mnożenia odwrotną transformację Fouriera. W rezultacie otrzymano:
c) przefiltrowany obraz , dla którego poziomy szarości pikseli mogą być liczbami zespolonymi,
d) obraz skompresowany (algorytmem JPEG).
b) przefiltrowany obraz, dla którego poziomy szarości pikseli należą do przedziału [0, 255],
a) obraz binarny, na którym otrzymano posegmentowane obrazy
Celem segmentacji jest:
d) wykrycie na obrazie prostoliniowych segmentów
c) połączenie kilku zdjęć w jeden większy obraz,
b) podział obrazu na rozdzielone od siebie obiekty,
a) usunięcie z obrazu szumów,
Przekształcenie watershed często wykorzystywane jest do:
b) podziału obiektów połączonych ze sobą,
d) wyliczania szkieletu obiektów.
a) eliminacji niewielkich obiektów,
c) zliczania obiektów które nie stykają się z brzegiem obrazu,
Przyłączanie do obszaru sąsiednich pikseli (lub obszarów) posiadających podobne cechy (tj. spełniających pewne kryterium jednorodności), to idea segmentacji:
b) z wykorzystaniem binaryzacji automatycznej,
d) przez rozrost.
c) przez podział,
a) z użyciem watershed,
Wykorzystywana w pomiarze długości obwodów obiektów formuła Croftona polega na:
d) wyliczeniu średniej z ilości pikseli po wewnętrznej i zewnętrznej stronie obwodu.
a) zliczaniu punktów brzegowych obiektu z uwzględnieniem wag,
b) przybliżaniu kształtu obiektu odpowiednim wielokątem,
c) pomiarze długości rzutów obiektu w 4 kierunkach,
Który z wyników najdokładniej podaje liczbę obiektów przypadająca na poniższe pole?
4
4.5
5.5
7


Cześć!
Wykryliśmy, że blokujesz reklamy na naszej stronie.
Reklamy, jak zapewne wiesz, pozwalają na utrzymanie i rozwój serwisu. W związku z tym prosimy Cię o ich odblokowanie by móc kontynuować naukę.
