500 pytań z fizyki

Praca wykonana przy rozciąganiu takiego układu sprężyn siłą zwiększającą się do F jest:

Stalowy drut został rozciągnięty o pewną małą długość x. Jakie musimy mieć jeszcze dane wielkości, aby obliczyć energią potencjalną sprężystości drutu?

Jaką siłą F należy rozciągnąć drut o przekroju S, aby jego długość nie uległa zmianie przy oziębieniu go o delta T ( n - moduł Younga, alfa - liniowy współczynnik rozszerzalności)?

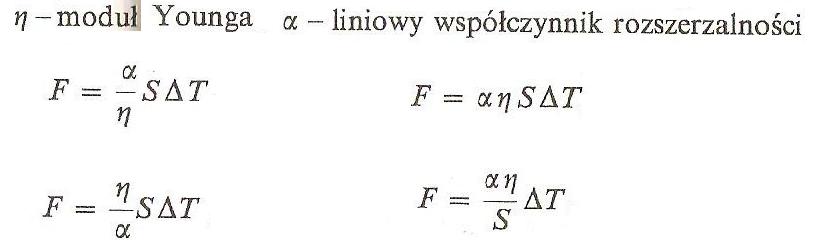
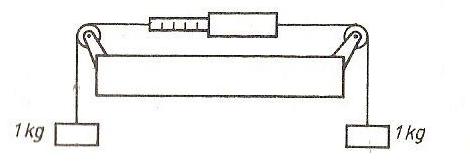
Na obu końcach wagi sprężynowej, pokazanej na rysunku zawieszono dwa ciężarki o masie 1 kg. Na podziałce wagi odczytamy:

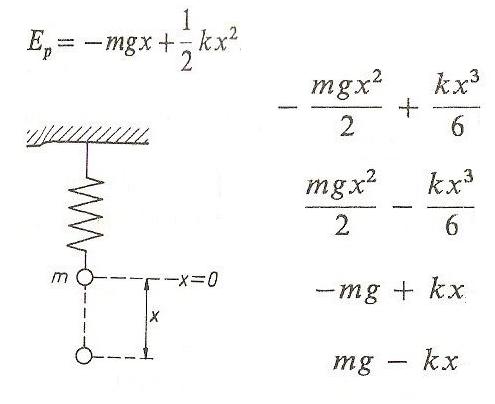
Energia potencjalna ciała jest dana wzorem Ep = -mgx + 1/2 kx^2. Siła działająca na to ciało w pozycji x jest dana wzorem:

Klocek, którego masę pomijamy przyczepiony do sprężyny (patrz rysunek) porusza się ruchem harmonicznym bez tarcia. Energia potencjalna tego układu jest równa zeru w położeniu równowagi, a maksymalna jej wartość wynosi 50J. Jeżeli wychylenie tego klocka z położenia równowagi wynosi 1/2 A (A - amplituda), to jego energia kinetyczna w tej chwili wynosi:

Zależność energii potencjalnej Ep od czasu t w ruchu harmonicznym przedstawiono na wykresie:

W ruchu wahadła nietłumionego<br /&rt;<br /&rt;1. całkowita energia mechaniczna jest stała<br /&rt;<br /&rt;2.energia kinetyczna w punkcie zawracania jest równa energii kinetycznej w punkcie zerowym (przechodzenie przez położenie równowagi)<br /&rt;<br /&rt;3. w każdej chwili energia kinetyczna jest równa energii potencjalnej<br /&rt;<br /&rt;4. energia potencjalna w punkcie zwracania jest równa energii kinetycznej w punkcie przechodzenia przez położenie równowagi<br /&rt;<br /&rt;Które z powyższych wypowiedzi są poprawne:<br /&rt;

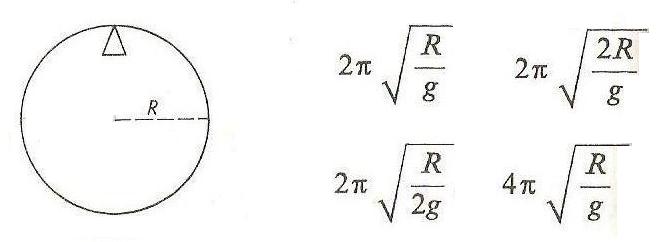
Okres drgań wahadła utworzonego z cienkiej obręczy o promieniu R i masie m zawieszonej na ostrzu, jak na rysunku obok wynosi:

Masa wahadła matematycznego wzrosła dwukrotnie, a jego długość zmalała czterokrotnie. Okres drgań wahadła:

Jeżeli długość wahadła zwiększymy dwukrotnie, to okres jego wahań:

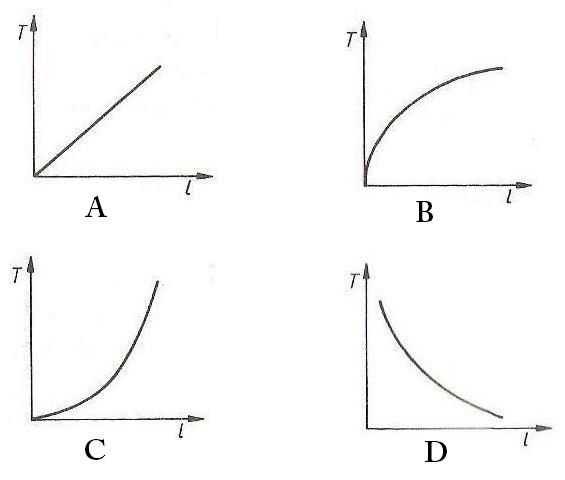
Zależność okresu drgań wahadła matematycznego T od jego długości l poprawnie przedstawiono na wykresie:

Na ciało o masie 1 kg, pozostające w chwili początkowej w spoczynku na poziomej płaszczyźnie działa równolegle do płaszczyzny siła 2 N. Współczynnik tarcia wynosi 0,1. Praca wykonana przez siłę wypadkową na drodze 1 m wynosi:<br /&rt;

Łyżwiarz poruszający się początkowo z prędkością 10 m/s przebywa z rozpędu do chwili zatrzymania się drogę 20 m. Współczynnik tarcia wynosi (przyjmując g = 10 m/s^2):<br /&rt;

Możemy wnioskować, że współczynnik tarcia statycznego linki o stół wynosi:

Ruch zsuwającej się ze stołu linki jest ruchem:

Samochód o masie m, poruszający się z prędkością v, może (na poziomej drodze) przejechać bez poślizgu zakręt o promieniu r ( f - współczynnik tarcia statycznego), jeżeli:

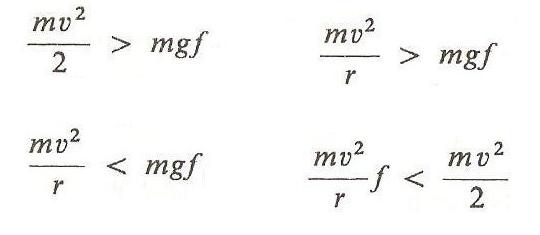
Na brzegu obracającej się tarczy leży kostka. Przy jakiej najmniejszej liczbie n obrotów na sekundę kostka spadnie z tarczy? ( f- współczynnik tarcia, d - średnica tarczy, g - przyspieszenie ziemskie)

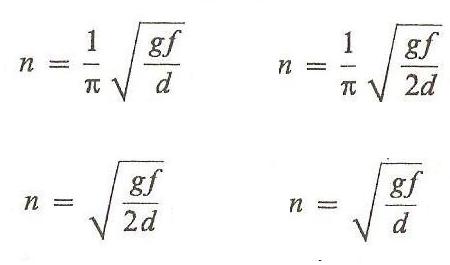
Kulka o masie m jest przyczepiona na końcu sznurka o długości R i wiruje w płaszczyźnie pionowej po okręgu tak, że w górnym położeniu nitka nie jest napięta. Prędkość tej kulki w chwili, gdy jest ona w dolnym położeniu wynosi:

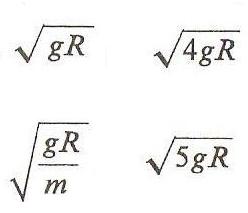
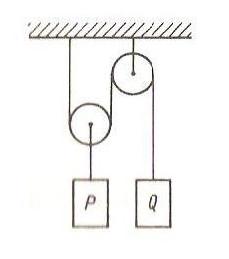
Układ przedstawiony na rysunku (masy bloczków i tarcie pomijamy) pozostaje w równowadze, jeżeli: