Podsumowanie
Prognozowanie procesów ekonomicznych
Podsumowanie
Prognozowanie procesów ekonomicznych
Twój wynik
Wszystkie ({{dataStorage.userResults.answersTotal}})
Prawidłowe ({{dataStorage.userResults.answersGood}})
Do powtórki ({{dataStorage.userResults.answersRepeat}})
Błędne ({{dataStorage.userResults.answersBad}})
Pytanie 1
Prognozowanie to:
przewidywanie teraźniejszości
przewidywanie przyszłości
przewidywanie przeszłości
Pytanie 2
Funkcja informacyjna polega na"
pobudzaniu do podejmowania odpowiednich działań
oswajaniu ludzi z nadchodzącymi zmianami, zmniejszaniu lęku przed przyszłością
wspomaganiu procesów decyzyjnych
Pytanie 3
Budowanie prognozy ekonomicznej jest tym bardziej uzasadnione, im:
krótszy jest horyzont czasowy
wyższy jest stopień inercji prognozowanej zmiennej
szybsze są zmiany prognozowanej wielkości
Pytanie 4
Do metod heurystycznych zaliczamy:
metodę delficką
metody analogowe
klasyczne modele trendu
Pytanie 5
Do wielorównaniowych modeli ekonometrycznych zaliczamy
modele proste
modele rekurencyjne
modele o równaniach współzależnych
Pytanie 6
Podział prognoz na długo-, średnio-, krótkoterminowe i bezpośrednie uzyskujemy w oparciu o kryterium
charakteru lub struktury
horyzontu czasowego
stopnia szczegółowości
Pytanie 7
Ze względu na cel (kryterium podziału) otrzymujemy prognozy:
samosprawdzające się i destruktywne
operacyjne i strategiczne
badawcze, w tym ostrzegawcze
Pytanie 8
Prognozowanie to przewidywanie przyszłości:
nieracjonalne
racjonalne i naukowe
racjonalne i zdroworozsądkowe
Pytanie 9
Prognoza to:
posiadana wiedza
przewidywanie
uprzednia wiedza
Pytanie 10
Ogół zasad i metod wnioskowania o przyszłości na podstawie odpowiedniego modelu ekonometrycznego, opisującego pewien wycinek sfery zjawisk ekonomicznych to:
prognoza
predykcja
estymacja
Pytanie 11
Trzy podstawowe funkcje prognoz to:
preparacyjna, aktywizujaca i informacyjna
preparacyjna, aktualizująca i informacyjna
opisująca, aktualizacyjna i informacyjna
Pytanie 12
Stworzenie, dzięki prognozie, dodatkowych przesłanek w procesie podejmowania racjonalnych decyzji gospodarczych, to funkcja
informacyjna
aktywizująca
preparacyjna
Pytanie 13
Jeżeli ogłoszenie prognozy powoduje podejmowanie działań sprzyjających realizacji prognozy korzystnej lub przeciwstawiających się realizacji prognozy niekorzystnej, to mamy do czynienia z funkcją:
aktywizującą
preparacyjną
informacyjną
Pytanie 14
Prognoza: "w przyszłym roku chętnych na studia dzienne w AE będzie więcej niż w bieżącym roku" jest prognozą:
ilościową
jakościową
ilościową i jakościową
Pytanie 15
Prognoza: "w przyszłym roku chętnych na studia dzienne w AE będzie więcej o 500 osó niż w bieżącym roku" jest prognozą:
ilościową i jakościową
ilościową
jakościową
Pytanie 16
Prognoza: "w przyszłym roku przyjęcia na studia magisterskie w AE będą odbywać się na podstawie konkursu świadectw" jest prognozą:
jakościową
ilościową i jakościową
ilościową
Pytanie 17
Wyprzedzenie czasowe prognozy (w stosunku do bieżącego okresu) jest równe realnemu wyprzedzeniu czasowemu prognozy wtedy i tylko wtedy, gdy:
opóżnienie w dopływie danych statystycznych jest równa zeru
czas niezbędny na podjęcie efektywnych kroków w celu skorygowania zarysowanych się niekorzystnych tendencji ekonomicznych jest równy zeru
długość horyzontu predykcji jest równa zeru
Pytanie 18
Prognozy dopuszczalne otrzymujemy wtedy, gdy
wyprzedzenie czasowe prognzoy ( w stos. do bieżącego okresu) nie przekracza długości horyzontu predykcji
realnie wyprzedzenie czasowe prognozy przekracza długość horyzontu predykcji
realne wyprzedzenie czasowe prognozy nie przekracza długości horyzontu predykcji
Pytanie 19
Spodziewana wartość odchyleń rzeczywistych realizacji zmiennej prognozowanej od prognoz to:
zarówno błąd ex post, jak i jego ocena ex ante
ocena ex ante błędu
błąd ex ante
Pytanie 20
Wartość odchyleń rzeczywistych realizacji zmiennej prognozowanej od obliczonych prognoz to:
błąd ex post
zarówno błąd ex post, jak i jego ocena ex ante
ocena ex ante błędu
Pytanie 21
Wybór modelu prognostycznego może zostać oparty na:
analizie materiału statystycznego
teorii ekonomicznej
doświadczeniu zdobytym w trakcie prowadzenia podobnych badań
Pytanie 22
Z dwóch konkurencyjnych modeli prognostycznych wybieramy ten, który charakteryzuje się
względnie łatwą estymacją parametrów modelu
brakiem interpretacji ekonomicznej parametrów modelu
niższym stopniem dokładności, z jaką model opisuje rozwój danego zjawiska w przeszłości
Pytanie 23
Dane statystyczne, na podstawie których szacuje się parametry modelu prognostycznego, powinny być
prawdziwe
aktualne
niejoednoznaczne
Pytanie 24
Klasyczne założenia teorii predykcji to m.in.:
stabilność lub prawie stabilność prawidłowości ekonomicznej w czasie
dopuszczalność ekstrapolacji modelu poza zaobserwowany w "próbie" obszar zmienności zmiennych objaśniających
stabilność rozkładu składnika losowego modelu
Pytanie 25
Znajomość modelu kształtowania się zmiennej prognozowanej (pierwsze klasyczne założenie teorii predykcji) oznacza m.in.:
znajomość wartości ocen parametrów strukturalnych modelu
stabilność rozkładu składnika losowego modelu
znajomość postaci analitycznej modelu
Pytanie 26
Zmodyfikowane założenia teorii predykcji to m.in.:
stabilność rozkładu składnika losowego
stabilność lub prawie stabilność prawidłowości ekonomicznych w czasie
dopuszczalność ekstrapolacji modelu poza zaobserwowany w "próbie" obszar zmienności zmiennych objaśniających
Pytanie 27
Prawie stabilność oznacza, że występują zmiany, ale:
ich wielkość i kierunek można ocenić
są one nieregularne
są one powolne
Pytanie 28
Rodzaje predykcji ilościowej to:
predykcja skalarna i wektorowa
predykcja punktów zwrotnych
predykcja punktowa i przedziałowa
Pytanie 29
Rodzaje predykcji jakościowej to:
predykcja przewyższeń
predykcja ciągów monotonicznych
predykcja punktowa i przedziałowa
Pytanie 30
Predykcja punktów zwrotnych polega na:
stwierdzeniu, ze w pewnym okresie zmienna prognozowana osiągnie wartość np. mniejszą od wyróżnionej liczby
daniu odpowiedzi na pytanie, czy w kolejnych okresach obserwowana tendencja, np. spadkowa, utrzyma się
przewidywaniu wystąpienia w pewnym okresie zmiany obecnej tendencji np. ze spadkowej na wzrostową
Pytanie 31
Zasadę predykcji nieobciążonej stosujemy wówczas, gdy:
predykcja ma charakter powtarzalny ( w dużych odstępach czasu)
predykcja ma charakter powtarzalny ( w małych odstępach czasu)
predykcja ma charakter jednorazowy
Pytanie 32
Zasada predykcji nazywana ekonomiczną to:
zasada predykcji wg największego prawdopodobieństwa
zasada minimalizacji oczekiwanej straty
zasada predykcji nieobciążonej
Pytanie 33
Zasada predykcji nieobciążonej i wg największego prawdopodobieństwa dają takie same prognozy, gdy zmienna prognozowana ma rozkład
symetryczny
asymetryczny lewostronnie
asymetryczny prawostronnie
Pytanie 34
Zmienną losową Dt = Yt - YPt nazywamy:
czystym błędem predykcji
pełnym błędem predykcji
błędem predykcji
Pytanie 35
Czysty błąd predykcji wyraża:
odchylenie zmiennej prognozowanej od modelu, który nie został jeszcze oszacowany
odchylenie zmiennej prognozowanej o prognozy opartej na modelu wolnym od błędów estymacji
odchylenie zmiennej prognozowanej od ustalonego modelu
Pytanie 36
Względny błąd predykcji określa:
o ile, średnie w długim ciągu predykcji, rzeczywiste realizacje zmiennej prognozowanej będą się odchylać od prognoz
jaki procent obliczonej prognozy wynosi średni błąd predykcji
o ile, średnio w długim ciągu predykcji, prognozy będą przeszacowane lub niedoszacowane
Pytanie 37
Miernikiem dokładności predykcji przedziałowej jest:
względna precyzja predykcji
wiarygodność predykcji
precyzja predykcji
Pytanie 38
Wiarygodność predykcji przedziałowej oznacza, ze:
100 x Yt procent prognozy punktowej stanowi precyzja predykcji przedziałowej
wystąpi maksymalny błąd prognozy predykcji
w długim ciągu predykcji około 100 x Yt procent prognoz przedziałowych będzie trafnych
Pytanie 39
Zwiększenie wiarygodności predykcji przedziałowej, przy stałym rozmiarze "próby", prowadzi do:
zmniejszenia wartości miernika precyzji predykcji
tego, że wartość miernika precyzji predykcji nie zmieni się
zwiększenia wartości miernika precyzji predykcji
Pytanie 40
Przez prognozę wygasłą rozumiemy prognozę obliczoną dla okresu, dla którego
nie jest znana prawdziwa wartość zmiennej
będzie znana prawdziwa wartość zmiennej
jest znana prawdziwa wartość zmiennej
Pytanie 41
Średnie obciążenie predykcji ex post w przypadku predykcji nieobciążonej jest
równe zeru
większe od zera
mniejsze od zera
Pytanie 42
Jeśli średnie obciążenie predykcji ex post jest mniejsze od zera, to oznacza, że prognozy są przeciętnie
niedoszacowane
przeszacowane
równe wartościom rzeczywistym
Pytanie 43
Średni błąd predykcji ex post określa
o ile średnio odchylają się realizacje zmiennej prognozowanej od obliczonych prognoz
jaki procent przeciętnej prognozy wynosi średnie obciążenie ex post predykcji
jaki procent przeciętnej rzeczywistej realizacji zmiennej prognozowanej stanowi średni błąd ex post predykcji
Pytanie 44
Składniki współczynnika Theila wskazują, że źródłem błędów predykcji może być m.in.:
niedostateczna predykcja punktów zwrotnych
wystarczająca elastyczność predykcji
obciążenie predykcji
Pytanie 45
O niedostatecznej elastyczności predykcji świadczy
niedostateczna zgodność średnich wartości rzeczywistych i prognoz
niedostateczna zgodność kierunku zmian wartości rzeczywistych i prognoz
niedostateczna zgodność poziomu zróżnicowania wartości rzeczywistych i prognoz
Pytanie 46
Współczynnik Janusowy służy do badania:
aktualności modelu prognostycznego
obciążenia modelu prognostycznego
elastyczności modelu prognostycznego
Pytanie 47
Względnymi miernikami dokładności ex post predykcji są:
współczynnik Theila i współczynnik Janusowy
względne obciążenie i względny błąd predykcji ex post
średnie obciążenie i średni błąd predykcji ex post
Pytanie 48
Błędy ex post predykcji powinny być:
niestacjonarne
nie ma znaczenia czy są stacjonarne, czy też niestacjonarne
stacjonarne
Pytanie 49
Jako ocenę składnika losowego modelu przyjmujemy
wartości prognoz wygasłych
wartość reszt modelu
wartości teoretyczne modelu
Pytanie 50
Średnia arytmetyczna reszt modelu z addytywnym składnikiem losowym powinna być równa
nie ma żadnej prawidłowości
zeru
jedności
Pytanie 51
Gdy wariancja składnika losowego jest duża to:
otrzymujemy bardzo dobre oszacowanie parametrów modelu
zbudowane prognozy są na pewno dopuszczalne
otrzymujemy model bardzo dobrze dopasowany do danych empirycznych
Pytanie 52
Horyzont prognozy to przedział postaci:
del. = delta
( tb, tb + del.^2 ]
( tn, tn + del.^2 ]
( tb, T ]
Pytanie 53
Horyzont predykcji (dla bieżącego okresu) to przedział postaci:
del. = delta
( tb, T ]
( tb, tb + del.^2 ]
( tn, tn + del.^2 ]
Pytanie 54
Horyzont predykcji (dla wyjściowego okresu prognozy) to przedział postaci:
( tn, tn + del.^2 ]
( tb, T ]
( tb, tb + del.^2 ]
Pytanie 55
Zasadę predykcji wg największego prawdopodobieństwa można zapisać w następujący sposób:
YPt - min E ( W ), gdzie W jest funkcją straty
YPt = M0 ( YT )
YPt = E ( YT )
Pytanie 56
Zasadę predykcji opartą na przedziale ufności można zapisać w następujący sposób:
YPt = E ( YT )
P (Yt "należy do" IPt) - yr
YPt = M0 ( YT )
Pytanie 57
Stopa bezrobocia w Polsce na koniec miesiąca od stycznia do września 2001 wynosiła 15,7; 15,9; 16,1; 16,0; 15,9; 16,0; 16,2; 16,3; 16,4; czy:
jest to przykład deterministycznego szeregu czasowego
jest to szereg czasowy okresów
jest to szereg czasowy momentów
Pytanie 58
Składowa systematyczna w szeregu czasowym może wystąpić w postaci
wahań sezonowych
wahań cyklicznych
trendu
Pytanie 59
Z działaniem przyczyn głównych związane jest występowanie w szeregu czasowym prognozowanej zmiennej:
stałego przeciętnego poziomu
składnika losowego
składowej perdiodycznej
Pytanie 60
Jeżeli każdy element szeregu czasowego można zapisać jako sumę składowych szeregu, to mamy do czynienia z modelem:
addytywnym
mieszanym
multiplikatywnym
Pytanie 61
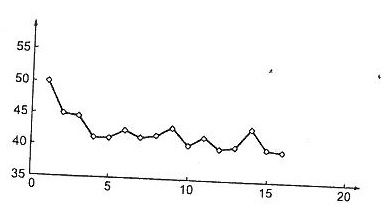
Na rysunku przedstawiono wykres szeregu czasowego pewnej zmiennej. Na jego podstawie możemy stwierdzić, że w szeregu tym występuje:
trend liniowy i wahania przypadkowe
tylko składowa przypadkowa
trend hiperboliczny i wahania przypadkowe
Pytanie 62
O istnieniu trendu wykładniczego można mówić wówczas, gdy na wykresie wzdłuż linii prostej układają się punkty o współrzędnych:
( e^2, yt )
( lnt, yt )
( t, ln yt )
Pytanie 63
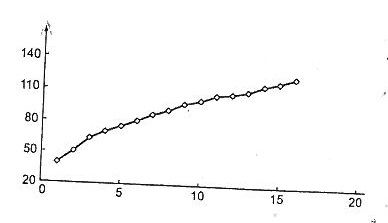
Na rysunku przedstawiono wykres szeregu czasowego pewnej zmiennej. Na jego podstawie możemy stwierdzić, ze w szeregu tym występuje:
składowa systematyczna w postaci trendu liniowego oraz składowa przypadkowa
tylko składowa systematyczna
składowa systematyczna w postaci trendu potęgowego oraz składowa przypadkowa
Pytanie 64
O istnieniu trendu potęgowego można mówić wówczas, gdy na wykresie wzdłuż linii prostej układają się punkty o współrzędnych:
( ln t, yt )
( ln t, ln yt )
( t, ln yt )
Pytanie 65
Za paraboliczną postacią trendu przemawiają w miarę stałe:
drugie przyrosty absolutne o podstawie zmiennej badanego zjawiska
drugie przyrosty absolutne o podstawie stałej badanego zjawiska
drugie przyrosty względne o podstawie zmiennej badanego zjawiska
Pytanie 66
Za wykładniczą postacią trendu przemawiają w miarę stałe:
indeksy o podstawie stałej, przy czym podstawą jest okres, dla którego zjawisko przyjmuje najmniejszą wartość
przyrosty względne o podstawie zmiennej badanego zjawiska
indeksy łańcuchowe
Pytanie 67
Za liniową postacią trendu przemawiają w miarę stałe:
przyrosty absolutne o podstawie zmiennej badanego zjawiska
przyrosty absolutne o podstawie stałej badanego zjawiska
przyrosty względne o podstawie zmiennej badanego zjawiska
Pytanie 68
W celu oszacowania parametrów funkcji trendu f(t) = t / a0 + a1t odpowiedni model sprowadzamy do postaci liniowej przez następującą transformację zmiennej y oraz t:
1/y oraz 1/t
lny oraz 1/t
modelu z taką funkcją trendu nie da się sprowadzić do postaci liniowej
Pytanie 69
Szereg czasowy przedstawia wartości pewnej zjawiska co kwartał. Na podstawie analizy graficznej jego przebiegu stwierdzamy, że co cztery kwartały wykazuje on podobne własności, zatem:
charakteryzuje się cyklem rocznym
charakteryzuje się wahaniami o okresie 4 kwartaly, czyli o okresie rocznym
charakteryzuje się wahaniami o okresie 1 kwartał
Pytanie 70
Metoda trendów jednoimiennych okresów polega na:
oszacowaniu wskaźników sezonowości dla poszczególnych faz cyklu
oszacowaniu parametrów funkcji trendu oddzielnie dla poszczególnych faz cyklu
oszacowanie parametrów funkcji trendu oddzielnie dla każdego cyklu
Pytanie 71
Do opisu szeregu czasowego zawierającego obserwacje z 24 kwartałów pewnej zmiennej wybrano analizę harmoniczną, czy:
pierwsza harmonika ma okres 6 lat
należy oszacować parametr 12 harmonik
szósta harmonika ma okres 1 roku
Pytanie 72
Suma bezwględnych wahań sezonowych (oczyszczonych)
zawsze jest równa zeru
zależy od tego, czy rozważamy wahania półroczne, kwartalne czy miesięczne
zawsze jest równa 100%
Pytanie 73
Suma wskaźników sezonowości (oczyszczonych)
zawsze jest równa 1
jest równa 4 w przypadku wahań kwartalnych
zawsze zależy od liczby cykli
Pytanie 74
Suma wskaźników sezonowości (oczyszczonych) w przypadku wahań miesięcznych
jest równa 12%
jest równa 12
jest równa 1200%
Pytanie 75
Suma oczyszczonych bezwzględnych wahań sezonowych (model addytywny) w przypadku wahań miesięczny
zależy od liczby cykli
jest równa 12
jest równa 0
Pytanie 76
Patrz obrazek
z kwartału na kwartał produkcja cementu przeciętnie wzrastała o 25,9 %
z roku na rok produkcja cementu średnio wzrastała o 25,9 [tys. ton]
z kwartału na kwartał produkcja cementu średnio wzrstałą o 25,9 [tys. ton]

Pytanie 77
prognoza produkcji cementu na czwarty kwartał 1997 r. wynosi 2951,52 [tys.ton]
prognoza produkcji cementu na czwarty kwartał 1997 r. wynosi 3365,52 [tys.ton]
prognozy nie można wyznaczyć, ponieważ nie jest znany bezwzględny wskaźnik sezonowości dla czwartego kwartału

Pytanie 78
Wykorzystując liniowy lub sprowadzalny do postaci liniowej model przyczynowo-opisowy można:
Na jego podstawie uzyskać prognozy wariantowe
Oszacować ex ante błędy wyznaczonych na jego podstawie prognoz
Ocenić siłę wpływu poszczególnych zmiennych na zmienną prognozowaną
Pytanie 79
Wady modelu przyczonowo-opisowego to:
Problemy przy estymacji parametrów związane z możliwością wystąpienia zjawiska współliniowości
Możliwość obliczenia prognoz wariantowych
Potrzeba wyznaczenia wartości zmiennych objaśniających w okresie na który buduje się prognozy
Pytanie 80
W celu wyboru postaci związku funkcyjnego f między zmienną objaśnianą a zmiennymi objaśniającymi przy budowaniu prognostycznego modelu przyczynowo-opisowego możemy wykorzystać:
Współliniowość zmiennych objaśniających
Istniejącą teorię na temat prognozowanego zjawiska
Analizę materiału statystycznego
Pytanie 81
W poprawnie zbudowanym modelu przyczynowo-opisowym”
Powinna występować silna korelacja między zmiennymi objaśniającymi
Zmienne objaśniające nie powinny być skorelowane ze zmienną objaśnianą
Zmienne objaśniające powinny być jak w najmniejszym stopniu skorelowane między sobą
Pytanie 82
Przy szacowaniu parametrów modelu przyczynowo-opisowego metodą najmniejszych kwadratów występowanie współliniowości zmiennych objaśniających jest zjawiskiem:
Pozytywnym, gdyż zazwyczaj otrzymujemy modele bardzo dobrze dopasowane do danych rzeczywistych
Neutralnym dla tej metody estymacji
Negatywnych, gdyż prowadzi do obniżenia efektywności estymatorów
Pytanie 83
Oszacowano pewien model przyczynowo-opisowy i okazało się ze spółczynnik determinacji jest „prawie” równy 1, ale jego parametry są statystycznie nieistotne. Przyczyną uzyskania takich wyników może być:
Współliniowość zmiennych objaśniających
Wysokie skorelowanie zmiennych objaśniających
Nie można nic powiedzieć o przyczynach takiego stanu rzeczy.
Pytanie 84
Zmienna objaśniająca w modelu przyczynowo-opisowym powinna:
Charakteryzować się dostatecznie dużą zmiennością czasową lub przestrzenno-czasową
Być silnie skorelowana ze zmienną objaśnianą
Charakteryzować się małą zmiennością czasową lub przestrzenno-czasową, gdyż gwarantuje to lepsze dopasowanie modelu do danych rzeczywistych
Pytanie 85
Oszacowanie ex ante średniego błędu predykcji prognozy wyznaczonej w poprzednim sprawdzianie (10) wynosi (po zaokrągleniu do 4 miejsc po przecinki):
10,2019
1,0555
1,1220
Pytanie 86
Na podstawie danych o kształtowaniu się liczby telefonów na 1000 mieszkańców w Polsce Yt (w tys. Szt) oraz liczby mieszkańców miast Polski Xt (w mln osób) w latach 1984-1997 oszacowano następujący model y^t = -147+12xt. ponadto liczbę mieszkańców miast Polski w latach 1984-1997 opisano modelem x^t = 19+0,3t
Na podstawie tych informacji prognoza liczby telefonów na 1999r wynosi 138,6
Na podstawie tych informacji prognoza liczby telefonów na 1998r wynosi 135
W celu wyznaczenia tej prognozy zastosowano model przyczynowo-opisowy
Pytanie 87
Kryterium podziału modelu wielorównaniowych na modele proste, rekurencyjne i równaniach współzależnych jest:
Obie wymienione wyżej macierze
Macierz T parametrów strukturalnych danego modelu stojących przy zmiennych z góry ustalonych
Macierz B parametrów strukturalnych danego modelu stojących przy zmiennych łącznie współzależnych
Pytanie 88
Jeżeli macierz B parametrów strukturalnych danego modelu wielorównaniowego stojących przy zmiennych łącznie współzależnych jest trójkątna to mamy do czynienia z modelem
Rekurencyjnym
Prostym
O równaniach współzależnych
Pytanie 89
Jeżeli macierz B parametrów strukturalnych danego modelu wielorównaniowego stojących przy zmiennych łącznie współzależnych jest diagonalna to mamy do czynienia z modelem
Prostym
Rekurencyjnym
O równaniach współzależnych
Pytanie 90
Predykcję łańcuchową stosujemy w przypadku wielorównaniowego modelu
Rekurencyjnego
O równaniach współzależnych
Prostego
Pytanie 91
Modele adaptacyjne znajdują zastosowanie w prognozowaniu
Krótkoterminowym
Długoterminowym
Średnioterminowym
Pytanie 92
Metodę średnich ruchomych można stosować w przypadku szeregów czasowych
Bez trendu i bez wahań okresowych
Z trendem i bez wahań okresowych
Bez trendu i z wahaniami okresowymi
Pytanie 93
przy obliczaniu prognozy metodą średniej ruchomej ważonej wartościom zmiennej:
można przypisać różne wagi
zawsze przypisuje się takie same wagi
nie przypisuje się wag
Pytanie 94
metody naiwne znajdują zastosowanie w prognozowaniu
średnioterminowym
krótkoterminowym
długoterminowym
Pytanie 95
prognozę dla zmiennej wykazującej tendencję wzrostową (spadkową) o pewien procent c * 100, w metodzie naiwnej, obliczamy ze wzoru postaci:
ypt = (1+c)yn
ypt = yn
ypt = yn + c
Pytanie 96
w metodzie wyrównywania wykładniczego wartość wygładzona (dla t>1) jest średnią ważoną:
Wartości rzeczywistej i poprzedniej wartości wygładzonej
Wartości rzeczywistej oraz poprzedniej wartości wygładzonej powiększonej o wygładzony przyrost
Wartość rzeczywistej i średniej ważonej kilku poprzednich wartości wygładzonych
Pytanie 97
W przypadku zmiennej charakteryzującej się częstymi i nieregularnymi zmianami trendu stała wygładzania α w metodzie wyrównywania wykładniczego przyjmuje wartość bliską
1/2
Jedności
Zeru
Pytanie 98
Prognozę w metodzie wyrównywania wykładniczego obliczamy ze wzoru:
ypt = y^n + hcn
ypt = y^n + h[δ0(y^n – y^n-1)+…+ δt(y^n-t – y^n-t)]
ypt = y^n + h(y^n – y^n-1)
Pytanie 99
w metodzie wyrównywania wykładniczego we wzorze na y^t role wagi przypisanej wartości rzeczywistej z okresu t-5 pełni wyrażenie
(1 – α)^5
α(1 – α)^t-5
α (1 – α)^5
Pytanie 100
metodę podwójnego wygładzania wykładniczego stosujemy w przypadku szeregów czasowych
z trendem nieliniowym
stacjonarnych
z trendem liniowym
Pytanie 101
w metodzie wyrównywania wykładniczo-autoregresyjnego wartość wygładzona (dla t>k) jest średnią ważoną:
wartości rzeczywistej i poprzedniej wartości wygładzonej
wartości rzeczywistej i średniej ważonej kilku poprzednich wartości wygładzonych
wartości rzeczywistej oraz poprzedniej wartości wygładzonej, powiększonej o wygładzony przyrost
Pytanie 102
etap wygładzania w metodzie wyrównywania wykładniczo-autoregresyjnego jest taki sam jak w metodzie wyrównywania wykładniczego gdy:
β1 = 1
α = ½
k = 1
Pytanie 103
w metodzie Holta wartość wygładzona (dla t>1) jest średnią ważoną:
wartości rzeczywistej i poprzedniej wartości wygładzonej
wartość rzeczywistej i średniej ważonej kilku poprzednich wartości wygładzonych
wartość rzeczywistej oraz poprzedniej wartości wygładzonej powiększonej o wygładzony przyrost
Pytanie 104
metoda trendu pełzającego znajduje zastosowanie w prognozowaniu
krótkoterminowym
długoterminowym
średnioterminowym
Pytanie 105
równań odcinkowych w metodzie trendu pełzającego z k=7 dla szeregu czasowego zawierającego 14 okresów, możemy wyznaczyć
14
8
7
Pytanie 106
Prognozę w metodzie trendu pełzającego z wagami harmonicznymi obliczamy ze wzoru
Ypt = y^n + hcn
Ypt = y^n+h(y^n-y^n-1)
Ypt = y^n + hw
Pytanie 107
Wagi harmoniczne dają
Monotonicznie malejące udziały dla informacji coraz bliższych ostatniemu wyrazowi badanego szeregu czasowego
Monotonicznie rosnące udziały dla informacji coraz bliższych ostatniemu wyrazowi badanego szeregu czasowego
Monotonicznie rosnące udziały dla informacji coraz dalszych od ostatniego wyrazu badanego szeregu czasowego
Pytanie 108
Błędy predykcji możemy oszacować ex ante w przypadku metody
Wintersa
Trendu pełzającego z wagami harmonicznymi
Holta

