Twój wynik: Teoria Ryzyka 1
Twój wynik
Wszystkie ({{dataStorage.userResults.answersTotal}})
Prawidłowe ({{dataStorage.userResults.answersGood}})
Błędne ({{dataStorage.userResults.answersBad}})
Pytanie 1
Analiza portfelowa opiera się na inwestycjach
długoterminowy
krótkoterminowych
spekulacyjnych
Pytanie 2
Teorię techniki inwestowania więcej niż jeden walor w celu zmniejszenia do zera ryzyka dywersyfikowalne go i zoptymalizowania przychodów i ryzyka inwestycji wyjaśnia
analizy portfelowej
analizy technicznej
analizy fundamentalnej
Pytanie 3
Harry M. Markowitz, William F. Sharpe, Merton Miller byli laureatami Nagrody Nobla w dziedzinie
ekonomii finansowej
teorii ryzyka
matematyki
Pytanie 4
Laureaci Nagrody banku Szwecji imienia Alfreda Nobla w dziedzinie ekonomii za pionierskie prace w dziedzinie teorii ekonomii finansowej to
Harry M. Markowitz oraz William F. Sharpe
Oskar Morgenstern
John von Neumann
Pytanie 5
Nagrodę Nobla w dziedzinie ekonomi w 2002 roku dostali
John von Neumann
Oskar Morgenstern
Daniel Kahneman i Amos Tversky
Pytanie 6
Przykładami funkcji użyteczności są
Funkcja liniowa i wymierna
Funkcja logarytmiczna i wykładnicza
Funkcja potęgowa i kwadratowa
Pytanie 7
Obserwacje zachowań ludzkich potwierdzają tezę, że ludzi cechuje
malejąca, bezwzględna awersja do ryzyka oraz malejąca, względna awersja.
malejąca, bezwzględna awersja do ryzyka oraz stała lub malejąca, względna awersja.
malejąca, bezwzględna awersja do ryzyka oraz stała lub rosnąca, względna awersja.
Pytanie 8
Jeżeli inwestor wykazuje stałą, względną awersję do ryzyka,
wtedy bezwzględna awersja do ryzyka jest stała.
wtedy bezwzględna awersja do ryzyka rośnie.
wtedy bezwzględna awersja do ryzyka maleje.
Pytanie 9
Jeżeli inwestor charakteryzuje się malejącą względną awersją do ryzyka, to wraz ze wzrostem swojej zamożności będzie przeznaczał na ten cel coraz
mniejszą część posiadanych środków
większą część posiadanych środków
Pytanie 10
Jeśli inwestor charakteryzuje się rosnącą bezwzględną awersją do ryzyka, wówczas wraz ze wzrostem poziomu swej zamożności będzie przeznaczał coraz
więcej pieniędzy na ryzykowne inwestycj
mniej pieniędzy na ryzykowne inwestycje
Pytanie 11
Jeśli inwestor charakteryzuje się malejącą bezwzględną awersją do ryzyka, wówczas wraz ze wzrostem poziomu swej zamożności będzie przeznaczał coraz e
mniej pieniędzy na ryzykowne inwestycj
więcej pieniędzy na ryzykowne inwestycj
Pytanie 12
Miary awersji do ryzyka
Bezwzględna awersja do podejmowania ryzyka
wariancja
Względna awersja do podejmowania ryzyka
Pytanie 13
W zależności od poziomu awersji do ryzyka inwestorzy oczekują
różnej stopy zwrotu z ryzykownej inwestycji.
takiej samej stopy zwrotu z ryzykownej inwestycji.
Pytanie 14
Preferujemy loterię pierwszą nad drugą wtedy i tylko wtedy gdy wartość funkcji użyteczności dla pierwszej loterii jest większa od drugiej.
Jest to twierdzenie o
użytcznośći
zmienych losowych
reprezentacji
Pytanie 15
Twierdzenie o reprezentacji jest autorstwa
von Neumann'a i Morgenstern'a
Pierre’a Simona de Laplace’a
Daniela Bernaouli
Pytanie 16
Z dwóch loterii o tej samej parze możliwych wyników lepsza jest ta, przy której prawdopodobieństwo lepszego wyniku jest większe .
Monotoniczność
Podstawialność
Rozkładu loterri złożonych
Pytanie 17
Loteria powstająca wskutek zamiany w pewnej innej loterii wyniku ai na jednakowo dobry wynik b nie jest ani lepsza ani gorsza od loterii wyjściowej. Jest to aksjomat
Rozkładu loterri złożonych
Podstawialność
Podstawialność
Pytanie 18
Każdy wynik „pośredni” między dwoma innymi jest tak samo dobry, jak pewna loteria o tych dwóch możliwych wynikach. Jest to aksjomat
Przechodniość
Rozkładu loterri złożonych
Ciągłości
Pytanie 19
Loterie, których wynikami są loterie są równoważne odpowiednim loteriom ze „zwykłymi” wynikami i prawdopodobieństwami wyznaczonymi zgodnie z zasadami rachunku prawdopodobieństwa. Jest to aksjomat
Przechodniość
Ciągłości
Rozkładu loterri złożonych
Pytanie 20
Każde dwie loterie są porównywalne. Jest to aksjomat
Rozkładu loterri złożonych
Ciągłości
Przechodniość
Pytanie 21
Loterie, których wynikami są loterie są równoważne odpowiednim loteriom ze „zwykłymi” wynikami i prawdopodobieństwami wyznaczonymi zgodnie z zasadami rachunku prawdopodobieństwa.
Prawda
Fałsz
Pytanie 22
Podział ze względu na warunki w jakich decyzja jest podejmowana:
w warunkach będących kombinacją ryzyka i niepewności
w warunkach niepewności
w warunkach pewności
w warunkach ryzyka
Pytanie 23
Podział ze względu podmiot podejmujący decyzję
w warunkach niepewności
indywidualne
zbiorowe
Pytanie 24
Teoria gier jest dziedziną zajmującą się opisem różnych sytuacji, w których uczestniczą podmioty świadomie podejmujące pewne decyzje w wyniku których następują rozstrzygnięcia mogące zmienić ich położenie.
Paradoks użyteczności
Paradoks petersburski
Teoria użyteczności
Pytanie 25
Teoria użyteczności (utility)jest autorstwa
Pierre’a Simona de Laplace’a
Daniel Bernoulli
John'a von Neumann i Oskar'a Morgenstern
Pytanie 26
Paradoks petersburski jest autorstwa
John'a von Neumann i Oskar'a Morgenstern
Pierre’a Simona de Laplace’a
Daniel Bernoulli
Pytanie 27
Wzór Bayesa
Prawdopodobieństwo warunkowe
Prawdopodobieństwo całkowite
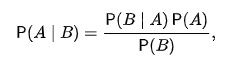
Pytanie 28
Prawdopodobieństwo warunkowe
Wzór Bayesa
Prawdopodobieństwo całkowite
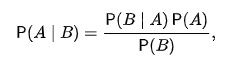
Pytanie 29
Wzór Bayesa
Prawdopodobieństwo warunkowe,
Prawdopodobieństwo całkowite
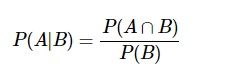
Pytanie 30
Miara rozproszenia wartości zmiennej wokół wartości oczekiwanej, którą oblicza się ze wzoru:
Wartość oczekiwana
Wariancja
Pytanie 31
Jest wartością, wokół której skupiają się wartości zmiennej losowej przy wielokrotnym powtarzaniu eksperymentu.
Wariancja
Wartość oczekiwana
Pytanie 32
Z rozkładem każdej zmiennej losowej związane są pewne charakteryzujące go wielkości liczbowe. Charakterystyki te nazywa się
parametrami rozkładu zmiennej losowej
zbiorem rozkładu zmiennej losowej
Pytanie 33
Zmienna losowa ciągła charakteryzowana jest za pomocą
funkcji gęstości rozkładu.
funkcji prawdopodobieństwa
Pytanie 34
Dodatkowo, oprócz dystrybuanty zmienna losowa dyskretna charakteryzowana jest za pomocą
funkcji gęstości rozkładu.
funkcji prawdopodobieństwa
Pytanie 35
Niezależnie od typu, każdą zmienną losową X można jednoznacznie określić za pomocą teoretycznej
zmiennej losowej
dystrybuanty
Pytanie 36
Jeśli zmienna losowa przyjmuje dowolne wartości z pewnego przedziału liczbowego, to nazywamy ją
zmienną losową ciągłą
dyskretną
Pytanie 37
Jeżeli zbiór wartości zmiennej losowej jest zbiorem przeliczalnym lub skończonym, wówczas zmienną losową nazywamy
zmienną losową ciągłą.
dyskretną
Pytanie 38
Wartości zmiennej losowej nie możemy z góry przewidzieć Ponieważ zależy Ona od przyczyn losowych
Fałsz
Prawda
Pytanie 39
Funkcję określoną na przestrzeni zdarzeń elementarnych, przyporządkowującą każdemu zdarzeniu elementarnemu liczbę rzeczywistą z określonym prawdopodobieństwem nazywamy
zbiorem elementów
zmienną losową
prawdopodobieństwem
Pytanie 40
Prawdopodobieństwem nazywamy funkcję P określoną na zdarzeniach taką, że
P(AÈ B) = P(A) + P(B) dla dowolnych, wykluczających się zdarzeń A, B
P(W) = 0
P(W) = 1
P(A) >= 0 dla dowolnego zdarzenia A,
Pytanie 41
Gra losowa, która mimo posiadania nieskończonej wartości oczekiwanej posiada jednocześnie ograniczoną wartość pieniężną dla większości ludzi
paradoks londyński
paradoks paryski
paradoks petersburski
Pytanie 42
Osobą która stworzyła podstawy rachunku prawdopodobieństwa i przyczyniła się do rozwoju rachunku różniczkowego i wariacyjnego jest
Pierre Simona de Laplace
Jakub Bernoulli
Pytanie 43
Kryterium podejmowania decyzji według którego należy wybrać decyzję, której odpowiada najwyższa oczekiwana wypłata, przy założeniu, że wszystkie stany natury są jednakowo prawdopodobne jest
autorstwa Hurwicza
autorstwa Pierre’a Simona de Laplace’a
autorstwa Bernoulliego
Pytanie 44
Jeżeli przy dużej liczbie prób, częstość zdarzenia dąży do jego rzeczywistego prawdopodobieństwa jest to
Prawo Wielkich Liczb
Prawo de Laplace
prawo Bernoulliego
Pytanie 45
Iloraz liczby zdarzeń sprzyjających zdarzeniu A do liczby wszystkich możliwych przypadków, zakładając, że wszystkie przypadki wzajemnie się wykluczają i są jednakowo możliw nazywamy
przestrzenią zdarzeń elementarnych
prawdopodobieństwem
zdarzeniem losowym
Pytanie 46
Mierzalny podzbiór A zbioru zdarzeń elementarnych danego doświadczenia losowego to
przestrzeń zdarzeń elementarnych
przestrzeń zdarzeń losowych
zdarzenie losowe
Pytanie 47
Zbiór wszystkich możliwych wyników doświadczenia losowego to
przestrzeń zdarzeń teoretycznych
przestrzeń zdarzeń elementarnych
przestrzeń zdarzeń doświadczalnych
Pytanie 48
Przykładem rachunku prawdopodobieństwa jest zut monetą, rzut kostką do gry, losowanie karty z talii kart, itp.
Prawda
Fałsz
Pytanie 49
Doświadczenie jest losowe
wyniku doświadczenia potrafimy z góry przewidzieć.
żeli można je wielokrotnie powtarzać w tych samych warunkach
wyniku doświadczenia nie potrafimy z góry przewidzieć.
Pytanie 50
Dział matematyki zajmujący się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe.
Ekonomia prawdopodobieństwa
Rachunek prawdopodobieństwa
Teoria prawdopodobieństwa

