Wyszukaj
Zaloguj / zarejestruj się
Jeśli masz już konto, możesz się zalogować.
Jeśli nie masz konta, zarejestruj nowe podając nazwę użytkownika, adres email i hasło.
Formularz kontaktowy
Memorizer+
Wykup dostęp
Ta funkcja jest dostępna dla użytkowników, którzy wykupili plan Memorizer+
Fiszki
500 pytań z fizyki
Test w formie fiszek Zbiór pytań i zadań z fizyki. Ogromna ilość pytań testowych do rozwiązania.
Ilość pytań: 234 Rozwiązywany: 69049 razy
Jeżeli moment bezwładności koła zamachowego, wykonującego n obrotów na sekundę, ma wartość I, to energia kinetyczna koła wynosi:
pi^2 n^2 I
2 pi^2 n^2 I
1/2 pi n I
1/2 pi n^2 I
Poziomo ustawiony pręt o długości l mogący się obracać wokół osi poziomej przechodzącej przez koniec pręta i prostopadłej do niego puszczono swobodnie. Moment bezwładności pręta względem osi przechodzącej przez jego ośrodek Io = 1/12 ml^2. Wartość prędkości liniowej końca pręta przy przejściu przez położenie równowagi wynosi:
pierw (3gl)
pierw (12gl)
pierw (2gl)
pierw (4gl)
Gaz doskonały to ośrodek, którego cząsteczki traktujemy jako:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
przyciągające się nawzajem obiekty, obdarzone masą i różną od zera objętością
punkty pozbawione masy
nie oddziaływające ze sobą obiekty, mające różną od zera objętość
obdarzone masą i nie oddziaływające wzajemnie punkty
Ciśnienie wywierane przez cząsteczki gadu doskonałego na ścianki naczynia zamkniętego zależy:
od liczby cząsteczek przypadających na jednostkę objętości gazu i od średniej energii potencjalnej cząsteczek
od liczby cząsteczek przypadających na jednostkę objętości gazu, od rodzaju gazu i od średniej energii kinetycznej gazu
od średniej energii kinetycznej i potencjalnej cząsteczek gazu
od liczby cząsteczek przypadających na jednostkę objętości gazy i od średniej energii kinetycznej cząstek gazu
Ciśnienie gazu doskonałego zależy od:<br /&rt;<br /&rt;1. średniej prędkości cząsteczek<br /&rt;2. liczby cząsteczek w jednostce objętości<br /&rt;3. średnicy cząsteczek<br /&rt;4. masy cząsteczek<br /&rt;<br /&rt;Które z powyższych odpowiedzi są poprawne?
tylko 1, 2 i 3
tylko 1 i 2
tylko 1, 2 i 4
wszystkie 1, 2, 3 i 4
W jednym naczyniu znajduje się 1 mol wodoru, a w drugim 1 mol tlenu o tej samej temperaturze. Objętości tych naczyń są jednakowe. Możemy wnioskować, że:<br /&rt;<br /&rt;<br /&rt;
ciśnienie wywierane przez wodór jest mniejsze, bo cząsteczki wodoru mają mniejszą masę od cząsteczek tlenu
ciśnienia obu gazów są równe
ciśnienie wywierane przez wodór jest większe, ponieważ cząsteczki wodoru mają większą prędkość niż cząsteczki tlenu o tej samej temperaturze
ciśnienia obu gazów są równe, ale tylko wtedy, gdy oba naczynia mają identyczne kształty (jednakowe wielkości ścianek)
W zamkniętym pojemniku znajduje się gaz o temperaturze T0. Do jakiej temperatury należy do ogrzać, aby podwoić średnią prędkość jego cząsteczek?
4 T0
4 pierwT0
2 T0
T0 pierw2
Walec stacza się bez poślizgu z równi pochyłej. Chwilowe przyspieszenie kątowe w ruchu walca nadaje moment:
siły tarcia lub siły ciężkości w zależności od wyboru osi obrotu
wypadkowej siły tarcia i ciężkości
zawsze tylko siły ciężkości
zawsze tylko siły tarcia
Jeżeli cząsteczki wodoru i atomy helu mają taką samą średnią prędkość ruchu postępowego, to możemy wnioskować, że między temperaturą wodoru T1 i temperaturą helu T2 zachodzi w przybliżeniu związek:
T1 = 0,5 T2
T1 = 0,25 T2
T1 = T2
T1 = 2 T2
Ciśnienie gazu doskonałego wzrosło w przemianie izochorycznej dwukrotnie i wobec tego:
średnia prędkość cząsteczek wzrosła dukrotnie
żadna z powyższych odpowiedzi nie jest poprawna
średnia energia kinetyczna cząsteczek wzrosła dwukrotnie
średnia energia kinetyczna cząsteczek zmalała dwukrotnie
Dla jednorodnego gazu doskonałego są dane: m - masa, V - objętość, p - ciśnienie, T-temperatura, R - stała gazowa (dla jednego mola). Masa gramocząsteczki wynosi:
mR / pVT
mRpV / T
mRT / pV
mpV / RT
Dla jednorodnego gazy doskonałego są dane: m - masa, V - objętość, p - ciśnienie, T - temperatura, R - stała gazowa (dla jednego mola), N - liczba Avogadra. Masa jednej cząsteczki wynosi:
mRVT / N
mRT / NpV
mpRT / NV
mpV / NRT
Jeżeli są dane: p - ciśnienie gazu, y - masa jednego mola tego gazu, R - stała gazowa, T - temperatura, to gęstość gazu równa się:
yp / RT
yR / pT
p / yRT
pR / yT
W wyniku przeprowadzonych przemian gazu doskonałego początkowe parametry p0, V0, T0 uległy zmianie na 2p0, 3V0, T. Jeżeli naczynie było szczelne, to T wynosi:
6 T0
2 T0
2/3 T0
3/2 T0
Na rysunku poniższym przemiany izotermiczną i izochoryczną przedstawiają: (p -ciśnienie, V - objętość)
prosta 4 i krzywa 1
prosta 3 i prosta 4
prosta 3 i krzywa 1
krzywa 1 i prosta 2
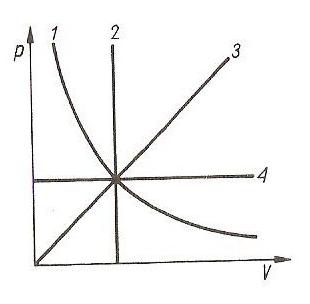
Na którym z poniższych wykresów nie przedstawiono przemiany izobarycznej? (p -ciśnienie, V - objętość, t - temperatura)
C
B
A
D
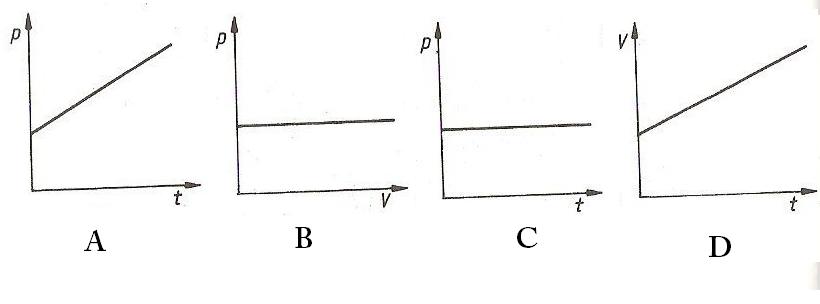
Która z dwóch izochor 1 i 2, przedstawionych na wykresie i sporządzonych dla tej samej masy gazu odpowiada większej objętości (w obu przypadkach mamy ten sam gaz)?
obie odpowiadają tej samej objętości
izochora 2
izochora 1 lub izochora 2, a zalęzy to od wartości dostarczonego ciepła
izochora 1
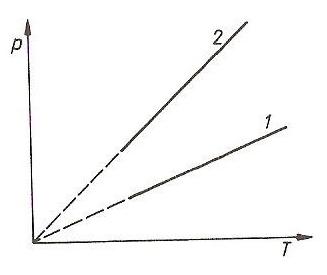
Na rysunku przedstawiono przemianę gazu doskonałego (p - ciśnienie, T - temperatura). O objętościach gazu w stanach 1, 2, 3 można powiedzieć:
V1<V2 i V2<V3
V1=V2 i V2>V3
V1<V2 i V1<V3
V1>V2 i V1=V3
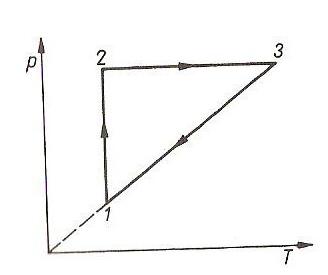
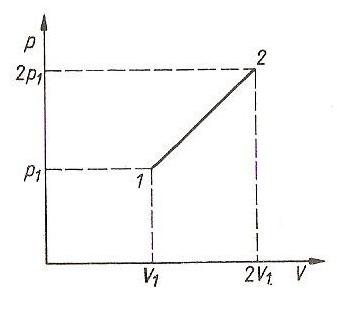
W przemianie określonej ilości gazu doskonałego, przedstawionej na rysunku, zachodzą następujące relacje między temperaturami T1 w stanie 1 i T2 w stanie 2:
T1 = 4T2
T2 = 2T1
T1 = T2
T2 = 4T1
W przemianie izochorycznej określonej ilości gazu doskonałego jego gęstość:
podczas wzrostu temperatury gaz maleje, a podczas obniżania temperatury rośnie
pozostaje stała pod warunkiem, że wzrost temperatury nie powoduje dysocjacji cząsteczek
podczas wzrostu ciśnienia wzrasta, a podczas obniżania ciśnienia maleje
nie ulega zmianie

Cześć!
Wykryliśmy, że blokujesz reklamy na naszej stronie.
Reklamy, jak zapewne wiesz, pozwalają na utrzymanie i rozwój serwisu. W związku z tym prosimy Cię o ich odblokowanie by móc kontynuować naukę.
