Fiszki
500 pytań z fizyki
Test w formie fiszek Zbiór pytań i zadań z fizyki. Ogromna ilość pytań testowych do rozwiązania.
Ilość pytań: 234
Rozwiązywany: 67703 razy
Na dwustronnej dźwigni wiszą na nitkach dwie kule o równych masach wykonane z dwóch materiałów o różnych gęstościach d1 < d2,przy czym obie gęstości są większe od gęstości wody dw. W powietrzu dźwignia jest w równowadze. Jeżeli kule wiszące na dźwigni zanurzymy do wody to:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
przeważa kula o większej gęstości d2
równowaga nie zostanie zachwiana
przeważa kula o mniejszej gęstości d1
równowaga nie zostanie zachwiana tylko wtedy, gdy stosunek d1/dw = d2/d1
przeważa kula o większej gęstości d2
Korek zanurzony w wodzie i puszczony swobodnie wypływa na powierzchnię wody, poruszając się za stałym przyspieszeniem (przy pominięciu siły oporu). Jeżeli eksperyment taki przeprowadzimy w kabinie sztucznego satelity Ziemi , to korek:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
wypływa na powierzchnię ruchem jednostajnym
pozostanie zanurzony w wodzie
wypływa na powierzchnię ruchem jednostajnie przyspieszonym z większym przyspieszeniem niż na Ziemi
wypływa na powierzchnię ruchem jednostajnie przyspieszonym z tą samą wartością przyspieszenia co na Ziemi
pozostanie zanurzony w wodzie
Można tak dobrać stężenie roztworu soli, aby wszystkie świeże jajka pływały w roztworze całkowicie zanurzone. Ten przypadek zachodzi wtedy, gdy następujące wielkości dla wszystkich jajek są równe:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
masy
objętości
kształty
gęstości
gęstości
Podnośnik hydrauliczny jest wyposażony w dwa cylindry o średnicach 1 cm i 5 cm. Aby większy mógł podnieść 100 N mniejszy tłok trzeba nacisnąć siłą:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
50 N
40 N
4 N
20 N
4 N
Ciśnienie słupa wody o wysokości 10 cm wynosi w układzie SI około:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
980 Pa
98 PA
9,8 Pa
10 ^-1 PA
980 Pa
Na dnie szerokiego naczynia znajduje się cienka warstwa rtęci. Jeżeli naczynie z rtęcią znajdzie się w stanie nieważkości to:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
rtęć przyjmie kształt płaski bez menisku
warstwa rtęci oderwie się od dna bez zmiany kształtu
pozostanie warstwą rtęci, ale menisk będzie bardziej wypukły
rtęć przyjmie kształt prawie kulistej kropli
rtęć przyjmie kształt prawie kulistej kropli
Ile obrotów na sekundę wykonują koła roweru o średnicy 0.4 m poruszającego się z prędkością 6,28 m/s?<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
50 s^-1
5 s^-1
1,57 s^-1
25,12 s^-1
5 s^-1
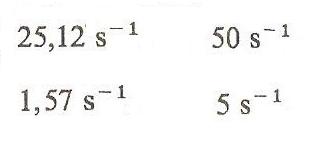
Jeżeli koło zamachowe wykonujące początkowo 12 obrotów na sekundę zatrzymuje się po 6 sekundach, to średnie przyspieszenie kątowe wynosi:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
- 2 pi s^-2
- 4 pi s^-2
- 2 s^-2
- 4 s^-2
- 4 pi s^-2
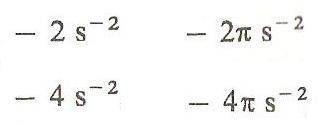
Tor zakreślony przez punkt materialny w obwodzie koła, które toczy się bez poślizgu jest cykloidą. Współrzędne toru tego punktu opisują następujące równania:<br /&rt;<br /&rt;x = wRt - Rsinwt, y = R- Rcoswt,<br /&rt;<br /&rt;gdzie R i w są stałymi, a t - czasem. Wartość przyspieszenia tej cząstki wynosi:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
2Rw^2
w^2 / R
2 / Rw^2
Rw^2
Rw^2
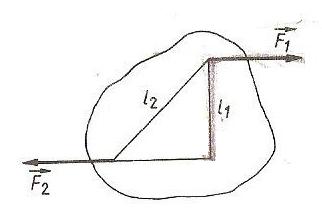
Na ciało działa para sił (F1 = F2 = F). Moment obrotowy tej pary sił ma wartość (l1 - odległość pomiędzy liniami sił), (l2 - odległość między punktami przyłożenia sił):
2F * l1
F * l2
F * l1
2F *l2
F * l1
Siła wypadkowa działająca na punkt materialny poruszający się ruchem jednostajnym po okręgu jest:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
różna od zera i skierowana od środka okręgu na zewnątrz
różna od zera i styczna do okręgu
różna od zera i skierowana do środka okręgu
równa zeru
różna od zera i skierowana do środka okręgu
Dwa dyski o momentach bezwładności I1 i I2 (przy czym I1 &rt; I2) obracają się tak, że ich energie kinetyczne są równe. Ich prędkości kątowe w1 i w2 oraz momenty pędu L1 i L2 są:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
w1 < w2 i L1 < L2
w1 = w2 i L1 &rt; L2
w1 &rt; w2 i L1 &rt; L2
w1 < w2 i L1 &rt; L2
w1 < w2 i L1 &rt; L2
Dane są dwie pełne kule A i B wykonane z tego samego materiału. Objętość kuli A jest ośmiokrotnie większa od objętości kuli B. Moment bezwładności względem osi przechodzącej przez środek masy kuli A jest:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
8 razy większy od momentu bezwładności kuli B
2 razy większy od momentu bezwładności kuli B
4 razy większy od momentu bezwładności kuli B
32 razy większy od momentu bezwładności kuli B
32 razy większy od momentu bezwładności kuli B
Jeżeli bryła sztywna wiruje wokół stałej osi i względem tej osi ma moment pędu L, a moment bezwładności I, to okres obrotu względem tej osi wynosi:
2pi L/I
2piIL
I / 2piL
2pi I/L
2pi I/L
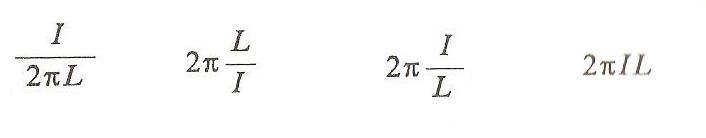
Bryła sztywna obraca się ze stałą prędkością kątową wokół nieruchomej osi symetrii. Zależność między energią kinetyczna bryły Ek a jej momentem pędu L i momentem bezwładności I można określić wzorem:
Ek = 1/2 L^2/I
Ek = 1/2 IL^2
Ek = 1/2 LI
Ek = L/I
Ek = 1/2 L^2/I
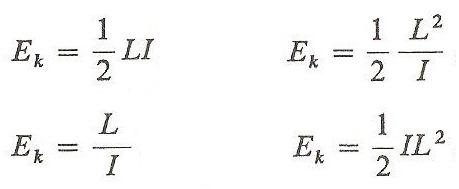
Co można powiedzieć o energiach kinetycznych ruchu postępowego Ekp i obrotowego Eko pełnego walca toczącego się po poziomej równi (moment bezwładności walca wynosi 1/2 mr^2).<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
Ekp < Eko
Ekp &rt; Eko
Ekp= Eko
Ekp &rt; Eko lub Ekp < Eko w zależności od masy walca
Ekp &rt; Eko
Człowiek siedzący na krześle obrotowym obraca się z prędkością kątową w (tarcie pomijamy) W wyciągniętych na boki rękach trzyma dwa różne ciężarki. Jeżeli człowiek opuści ręce to:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
moment pędu pozostanie nie zmieniony, a energia kinetyczna rośnie
moment pędu i energia kinetyczna zmaleją
ani energia, ani moment pędu nie mogą ulec zmianie ze względu na brak tarcia
moment pędu i energia kinetyczne wzrosną
moment pędu pozostanie nie zmieniony, a energia kinetyczna rośnie
Jeżeli wypadkowy moment sił działających na ciało obracające się wokół nieruchomej osi jest stały i różny od zera w czasie ruchu, to moment pędu (kręt) tego ciała:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
jednostajnie maleje lub wzrasta z czasem
jednostajnie wzrasta z czasem
pozostaje stały
jednostajnie maleje z czasem
jednostajnie maleje lub wzrasta z czasem
Cienki pręt o masie m i długości l obraca się wokół prostopadłej do niego osi. Jeżeli oś przechodzi przez koniec pręta, to moment bezwładności wynosi 1/3 ml^2; jeżeli natomiast oś przechodzi przez środek pręta, to moment bezwładności wynosi:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
ml^2 / 6
ml^2
ml^2 / 2
ml^2 / 12
ml^2 / 12
Łyżwiarz zaczyna się kręcić z wyciągniętymi ramionami z energią kinetyczną 1/2 Io w0^2. Jeżeli łyżwiarz opuści ramiona to jego moment bezwładności maleje do 1/3 Io, a jego prędkość kątowa wynosi:<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;<br /&rt;
3 w0
w0 / 3
w0 / pierw 3
pierw z 3 w0
3 w0