Wyszukaj
Zaloguj / zarejestruj się
Jeśli masz już konto, możesz się zalogować.
Jeśli nie masz konta, zarejestruj nowe podając nazwę użytkownika, adres email i hasło.
Formularz kontaktowy
Memorizer+
Wykup dostęp
Ta funkcja jest dostępna dla użytkowników, którzy wykupili plan Memorizer+
Fiszki
Teoria Ryzyka 1
Test w formie fiszek Teoria Ryzyka 1
Ilość pytań: 50 Rozwiązywany: 1023 razy
Loterie, których wynikami są loterie są równoważne odpowiednim loteriom ze „zwykłymi” wynikami i prawdopodobieństwami wyznaczonymi zgodnie z zasadami rachunku prawdopodobieństwa.
Prawda
Fałsz
Podział ze względu na warunki w jakich decyzja jest podejmowana:
w warunkach niepewności
w warunkach pewności
w warunkach ryzyka
w warunkach będących kombinacją ryzyka i niepewności
Podział ze względu podmiot podejmujący decyzję
indywidualne
w warunkach niepewności
zbiorowe
Teoria gier jest dziedziną zajmującą się opisem różnych sytuacji, w których uczestniczą podmioty świadomie podejmujące pewne decyzje w wyniku których następują rozstrzygnięcia mogące zmienić ich położenie.
Paradoks petersburski
Paradoks użyteczności
Teoria użyteczności
Teoria użyteczności (utility)jest autorstwa
Daniel Bernoulli
Pierre’a Simona de Laplace’a
John'a von Neumann i Oskar'a Morgenstern
Paradoks petersburski jest autorstwa
John'a von Neumann i Oskar'a Morgenstern
Daniel Bernoulli
Pierre’a Simona de Laplace’a
Wzór Bayesa
Prawdopodobieństwo warunkowe
Prawdopodobieństwo całkowite
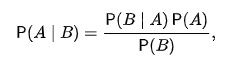
Prawdopodobieństwo całkowite
Wzór Bayesa
Prawdopodobieństwo warunkowe
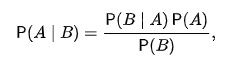
Prawdopodobieństwo warunkowe,
Wzór Bayesa
Prawdopodobieństwo całkowite
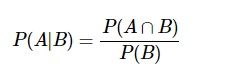
Miara rozproszenia wartości zmiennej wokół wartości oczekiwanej, którą oblicza się ze wzoru:
Wariancja
Wartość oczekiwana
Jest wartością, wokół której skupiają się wartości zmiennej losowej przy wielokrotnym powtarzaniu eksperymentu.
Wariancja
Wartość oczekiwana
Z rozkładem każdej zmiennej losowej związane są pewne charakteryzujące go wielkości liczbowe. Charakterystyki te nazywa się
parametrami rozkładu zmiennej losowej
zbiorem rozkładu zmiennej losowej
Zmienna losowa ciągła charakteryzowana jest za pomocą
funkcji gęstości rozkładu.
funkcji prawdopodobieństwa
Dodatkowo, oprócz dystrybuanty zmienna losowa dyskretna charakteryzowana jest za pomocą
funkcji prawdopodobieństwa
funkcji gęstości rozkładu.
Niezależnie od typu, każdą zmienną losową X można jednoznacznie określić za pomocą teoretycznej
dystrybuanty
zmiennej losowej
Jeśli zmienna losowa przyjmuje dowolne wartości z pewnego przedziału liczbowego, to nazywamy ją
zmienną losową ciągłą
dyskretną
Jeżeli zbiór wartości zmiennej losowej jest zbiorem przeliczalnym lub skończonym, wówczas zmienną losową nazywamy
zmienną losową ciągłą.
dyskretną
Wartości zmiennej losowej nie możemy z góry przewidzieć Ponieważ zależy Ona od przyczyn losowych
Fałsz
Prawda
Funkcję określoną na przestrzeni zdarzeń elementarnych, przyporządkowującą każdemu zdarzeniu elementarnemu liczbę rzeczywistą z określonym prawdopodobieństwem nazywamy
prawdopodobieństwem
zbiorem elementów
zmienną losową
Prawdopodobieństwem nazywamy funkcję P określoną na zdarzeniach taką, że
P(W) = 1
P(A) >= 0 dla dowolnego zdarzenia A,
P(AÈ B) = P(A) + P(B) dla dowolnych, wykluczających się zdarzeń A, B
P(W) = 0

Cześć!
Wykryliśmy, że blokujesz reklamy na naszej stronie.
Reklamy, jak zapewne wiesz, pozwalają na utrzymanie i rozwój serwisu. W związku z tym prosimy Cię o ich odblokowanie by móc kontynuować naukę.
